A forest is a hierarchical, node-based data structure. This document serves to cover the high-level concepts of a forest, adobe::forest<T> implementation details, as well as examples of frequent patterns.

Concepts

Terminology

$N$: An exemplar node

$P$: The parent node of $N$

$C$: A child node of $N$. The first and last children may also be termed $C_f$ and $C_l$, respectively.

$S$: A sibling node of $N$. The previous and next sibling may also be termed $S_p$ and $S_n$, respectively.

$R$: A root node

$I$: A forest (fullorder) iterator

Nodes

Forest’s fundamental element type is the node. They are heap-allocated by the forest as necessary for storing a value. Each node has exactly one parent and zero or more children. In this document we will draw nodes as circles:

The Root Node

Every forest has a root node, which is not a node used to store values in the forest. Rather, its primary purpose is as the anchor to which all top-level nodes in the forest are attached. In this document we will draw the root node as a rectangle:

Edges

Forest nodes are connected to one another with edges. For every node in the forest, there are exactly two edges that lead away from the node, and exactly two that lead towards the node. In this document edges will be drawn as arrows pointed in the direction of forward travel:

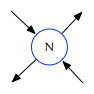
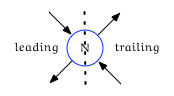
The two left edges are known as leading edges, and the two right edges are known as trailing edges:

The two edges that point to $N$ are known as in edges and the edges that point away from $N$ are out edges:

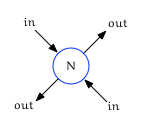
It is worth noting that the terms “in” and “out” are relative to $N$. In other words an in edge for $N$ will also be an out edge for some other node.

Leading In Edge

The northwest edge is the leading in edge. It originates from one of two related nodes:

• If $N$ is the first child of $P$, this edge comes from the leading edge of $P$:

  

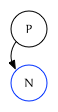
• Otherwise, this edge comes from the trailing edge of $N$’s prior sibling:

  

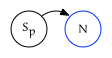
Leading Out Edge

The southwest edge is the leading out edge. Its points to one of two related nodes:

• If $N$ is a parent, it points to the leading edge of the first child of $N$.

  

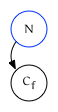
• Otherwise, it points to the trailing edge of $N$ itself:

  

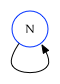
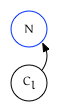
Trailing In Edge

The southeast edge is the trailing in edge. It originates from one of two related nodes:

• If $N$ is a parent, it comes from the trailing edge of $N$’s last child:

  

• Otherwise, it comes from the leading edge of $N$ itself:

  

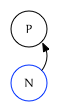
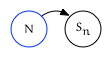
Trailing Out Edge

The northeast edge is the trailing out edge. It points to one of two related nodes:

• If $N$ is the last child of $P$, this edge points to the trailing edge of $P$:

• Otherwise, this edge points to the leading edge of $N$’s next sibling:

Example Forests

With the fundamental building blocks in place, here is how they combine to form some of the basic relationships in a forest. Note that (with the exception of the root node) every node in the forest maintains four relationships with the nodes around it.

Empty

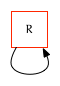
Given a forest that contains only the root node, forest<T>::empty will return true. Otherwise, it will return false.

One Node

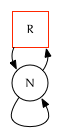
Two Sibling Nodes

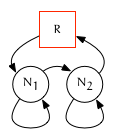
Iterators

Iterators are comprised of two pieces of data:

• the node to which they point
• the edge they are on

In this documentation Iterators will be described by this pair as {node, edge}.

Examples

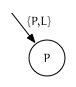
• {P, L} is an iterator that points to node $P$ on the leading edge:

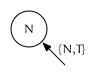
• {N, T} is an iterator that points to node $N$ on the trailing edge:

Since iterators always point to a node, we never speak of an iterator being on the “out” edge of a node it is from. Rather, we consider it on the “in” edge of the node that it points to (even though it’s the same edge).

Edge Flipping

You can use adobe::leading_of(I) and adobe::trailing_of(I) to change the edge of an iterator to leading or trailing, respectively. Note that these are free functions, not member functions of forest<T>. In this document we will represent these routines in pseudocode as such:

• leading_of({P, T}) → {P, L}
• trailing_of({N, L}) → {N, T}

Iterator Concept

Forest iterators are bidirectional. In this document we denote incrementing and decrementing an iterator with ++{node, edge} and --{node, edge}, respectively.

Iterator Adaptors

Although there is one iterator type for forest, there are several iterator adaptors that facilitate various methods of traversal. More will be said about these later.

A note on begin() and end()

begin() and end() in a forest behave just like their equivalent member functions found in a typical standard library container.

• forest<T>::end() will always return {R, T}. This is true regardless of whether or not the forest is empty.

• forest<T>::begin() will always return ++{R, L}. This follows the rules of the leading out edge explained above, meaning that it will either point to the first node in the forest (if it is not empty), or end() (if it is).

Forest Traversal

The root node is not considered during forest traversal. As such it is omitted from traversal diagrams.

Fullorder

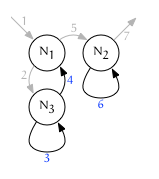
The default traversal behavior for a forest is fullorder. This means every node is visited twice: first, right before any of its children are visited (on the leading edge), and then again right after (on the trailing edge). This behavior is recursive, and results in a depth-first traversal of the forest:

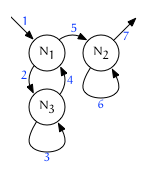
Here is the same diagram with the leading and trailing edges colorized:

Note that iteration 7 above has no color: it could be either {Sn, L} or {P, T}.

Fullorder traversal of $N$’s subtree

To traverse a node $N$ and all of its descendants, the iterator range is:

• leading_of({N, x}) → first
• ++trailing_of({N, x}) → last

Note this technique does not work if $N == R$.

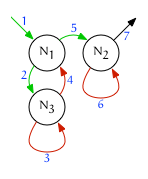
Preorder

A preorder traversal of the forest will visit every node once. During preorder traversal a parent will be visited before its children. Preorder iteration achieved by incrementing fullorder continually and visiting a node only when the iterator is on a leading edge:

• do ++{node, edge} while edge == trailing

Postorder

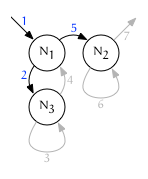
A postorder traversal of the forest will visit every node once. During postorder traversal a parent will be visited after its children. Postorder iteration achieved by incrementing fullorder continually and visiting a node only when the iterator is on a trailing edge:

• do ++{node, edge} while edge == leading

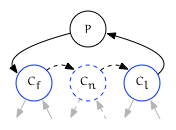
Child

A child traversal of a node $P$ traverses only its immediate children; $P$ itself is not visited. Child traversal is achieved by setting the edge of the iterator to trailing, then incrementing it:

• ++trailing_of({Cn, L}) → {Cn+1, L} (next child) or {P, T} (the end of the range)

Node Insertion

forest<T>::insert requires an iterator (where to insert) and a value (what to insert). The iterator is never invalidated during an insertion. insert returns a leading edge iterator to the new node.

Leading edge insertion

When the location for insertion is on the leading edge of $N$ (that is, $I$ is {N, L}) the new node will be created as $N$’s new previous sibling:

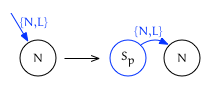
In this case insert returns {Sp, L}.

{N,T} can be used repeatedly to push back children of $N$.

Leading edge insertion can be used to repeatedly “push back” prior siblings of $N$. To repeatedly “push front” prior siblings of $N$, use the resulting iterator of insert as the next insertion position.

Trailing edge insertion

When the location for insertion is on the trailing edge of $N$ (that is, $I$ is {N, T}) the new node will be created as $N$’s new last child:

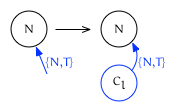
In this case insert returns {Cl, L}.

Trailing edge insertion can be used to repeatedly “push back” children of $N$. To repeatedly “push front” children of $N$, use the resulting iterator of insert as the next insertion position.

Algorithms & Examples

Detecting if $I_{node}$ is the first child of its parent

Given:

1. An iterator $I$ pointing to $I_{node}$
2. Its predecessor $H = –I$

If $I_{edge} == leading$ and $H_{edge} == leading$, then $I_{node}$ is the first child of $H_{node}$.

Pseudocode

bool is_first_child = (--leading_of({N, x})).edge() == leading

Visualization

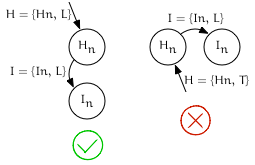
Detecting if $I_{node}$ is the last child of its parent

Given:

1. An iterator $I$ pointing to $I_{node}$
2. Its successor $J = ++I$ pointing to $I_{node}$

If $I_{edge} == trailing$ and $J_{edge} == trailing$, then $I_{node}$ is the last child of $J_{node}$.

Pseudocode

bool is_last_child = (++trailing_of({N, x})).edge() == trailing

Visualization

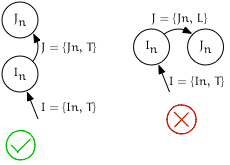
Detecting if $I_{node}$ has children

Given:

1. An iterator $I$ pointing to $I_{node}$
2. Its successor $J = ++I$ pointing to $J_{node}$

If $I_{edge} == leading$ and $J_{edge} == leading$, then $I_{node}$ has children (the first of which is $J_{node}$). Otherwise $I_{node}$ is a leaf node, and $I_{node} == J_{node}$.

Pseudocode

bool has_children = (++leading_of({N, x})).edge() == leading

Visualization

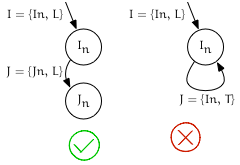
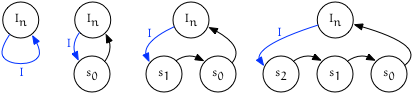
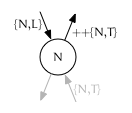
“Push back” children of $I_{node}$

Given:

1. An iterator $I = {node, trailing}$
2. A sequence of values $S$ to insert

We repeatedly insert subsequent values found in $S$ at position $I$.

Pseudocode

for (const auto& s : S) {
    forest.insert(I, s);
}

Visualization

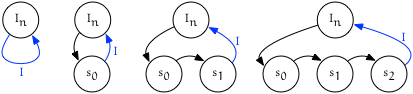
“Push front” children of $I_{node}$

Given:

1. An iterator $I = {node, trailing}$
2. A sequence of values $S$ to insert

We repeatedly insert subsequent values found in $S$ at position $I$, each time reassigning $I$ to be the result of the insertion.

Pseudocode

for (const auto& s : S) {
    I = forest.insert(I, s);
}

Visualization